MCM Week6 会议记录

CPMAP MCM 2025 C，奥运奖牌分析。

数据特征工程

特征工程 = 提升模型表达能力的“数据加工”过程，让数据更适合模型理解。 深度解析｜特征工程在推荐算法中的应用

1. 特征清洗（Feature Cleaning）

让数据“干净”“可用”：

• 缺失值处理（均值填补、回归填补、插值）
• 异常值处理（winsorize、IQR、z-score）
• 重复样本、噪声样本处理

📌 目标：让模型不会被垃圾数据误导。

2. 特征转换（Feature Transformation）

让特征“更好学”：

• 归一化（min-max）
• 标准化（z-score）
• 对数、平方根变换（处理偏态分布）
• 分箱（binning，可用于 LR、评分卡）

📌 目标：让模型更容易收敛，提高稳定性。

3. 特征构造（Feature Construction）

创造新的、更有价值的特征：

• 特征组合（乘积、差值、比值）
• 统计特征（均值、方差、最大值、趋势）
• 时间序列特征（滞后、滑动窗口）
• NLP 特征（TF-IDF、词向量 embedding）
• 图像特征（HOG/SIFT，或 CNN embedding）

📌 目标：让模型更容易捕捉数据规律。

4. 特征选择（Feature Selection）

从大量特征里挑出“最有用的几项”：

• Filter 方法（相关性、chi-square、信息增益）
• Wrapper 方法（RFE、逐步删除）
• Embedded 方法（L1/L2、树模型重要性）

📌 目标：降低维度、减少过拟合、提高速度。

5. 特征编码（Feature Encoding）

把“非数值信息”转成数值：

• One-hot 编码（类别特征 → 向量）
• Label Encoding（类别 → 整数）
• Target Encoding
• Embedding（深度学习用）

📌 目标：让模型理解类别信息。

---

主成分分析（PCA）

SHW - 主成分分析｜主成分分析原理讲解｜代码实现

深度学习入门算法之一，通过寻找数据中方差最大的方向，把原始特征线性组合成更少的新特征（主成分），尽可能保留原始信息。

目标

• 提取最有信息量的方向
• 去除噪声方向
• 将高维数据映射到低维（如 100 维 → 2 维）
• 让模型更快、更稳定

举例

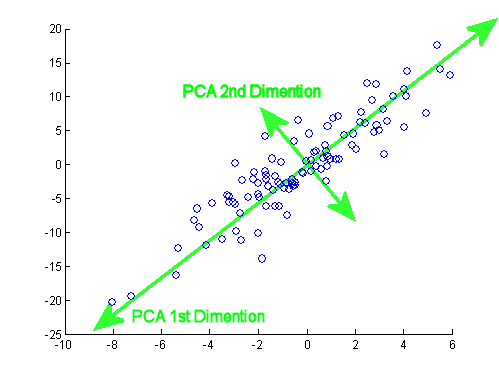
数据沿着 PCA1 方向变化最大，要找出这个方向。

数学步骤

给定数据矩阵 $X \in \mathbb{R}^{n \times d}$：

Step 1：去均值（中心化）

$$ X' = X - \bar{X} $$

Step 2：计算协方差矩阵

$$ C = \frac{1}{n-1} X'^T X' $$

Step 3：特征值分解

求解：

$$ C v_i = \lambda_i v_i $$

• $v_i$：特征向量（主成分方向）
• $\lambda_i$：特征值（信息量大小）

Step 4：选择最大的 k 个特征值对应的特征向量

按 $\lambda$ 从大到小排序。

Step 5：降维：投影到新空间

$$ Z = X' V_k $$

其中 $V_k$ 是前 k 个主成分组成的矩阵，从 $d$ 维降到 $k$ 维完成。

---

z-score

数据标准化算法：

$$ z = \frac{x - \mu}{\sigma} $$

经过 z-score 转换后，新的数据集会具有：

• 平均值（$\mu$）：恒为 0
• 标准差（$\sigma$）：恒为 1

---

机器学习：监督学习

参考资料

在机器学习领域，主要有三类不同的学习方法：

• 监督学习（Supervised learning）
• 非监督学习（Unsupervised learning）
• 半监督学习（Semi-supervised learning）

---

机器学习：决策树

CSDN 参考资料｜菜鸟教程

决策树（Decision Tree）：用特征阈值做判断的树结构，if-else 逐层分裂，叶子给出预测。

• 对于分类问题：叶子节点存类别或类别概率
• 对于回归问题：叶子节点存一个实数（平均值）

前置知识

Shwstone - 熵为什么是数据压缩的极限｜《深度学习》（Ian Goodfellow）3.13｜《机器学习》（周志华）第四章

信息量

假设一枚硬币是公平的，每次抛掷出现正面（Heads）的概率：

$$ P(H) = \frac{1}{2} $$

信息量（香农定义）：

$$ I(H) = -\log_2 P(H) = -\log_2\left(\frac{1}{2}\right) = 1 \text{ bit} $$

抛两次都是正面，信息量：

$$ I_{\text{total}} = I(H_1) + I(H_2) = 1 + 1 = 2 \text{ bits} $$

从概率角度：

$$ P(HH) = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4} \to I(HH) = -\log_2\left(\frac{1}{4}\right)=2\text{ bits} $$

信息熵

信息熵（entropy）：表示不确定性程度。不确定性越大，熵越大。纯度 (purity) 越高，熵越小。

$$ H(X) = -\sum_{x \in \mathbb{X}}{p(x) \log p(x)} $$

当 $\log$ 底数是 2 时，单位为 bit；底数为 $e$ 时单位为 nat。分布越接近均匀，$H(X)$ 越大。

KL 散度

$$ D_{\mathrm{KL}}(P \,\|\, Q) = \sum_{x \in \mathbb{X}} P(x) \log \frac{P(x)}{Q(x)} = \sum_{x \in \mathbb{X}} P(x)\bigl(\log P(x) - \log Q(x)\bigr). $$

只有 $P$、$Q$ 完全相同时 KL 散度为 0；KL 非对称，$D_{\mathrm{KL}}(p\|q)\neq D_{\mathrm{KL}}(q\|p)$（$p\neq q$）。

交叉熵

关系式：

$$ H(P,Q)=H(P) + D_{\mathrm{KL}}(P\|Q) $$

定义：

$$ H(P,Q) = -\sum_{x \in \mathbb{X}} P(x)\,\log Q(x) $$

性质：最小化交叉熵等价于最小化 KL 散度。约定 $0\log{0} = 0$。

单个样本数据集 $D$ 的熵

样本被分为 $K$ 类：

$$ H(D) = \mathrm{Ent}(D) = - \sum_{k=1}^{K} p_k \ln p_k $$

• $p_k$：样本数据集 $D$ 中，第 $k$ 类样本所占比例。

多个样本数据集的熵

有 $V$ 个样本数据集：

$$ \mathrm{Ent}(D_1, D_2, \ldots, D_V) = \sum_{v=1}^{V} \frac{|D_v|}{|D|} \, \mathrm{Ent}(D_v) $$

• $D = D_1 \cup D_2 \cup \cdots \cup D_V$
• $|D_v|$：集合 $D_v$ 中的样本个数
• $|D|$ ：集合 $D$ 中的样本个数

决策树核心

分类

序号	算法	关键指标	特点	树类型
1	ID3	信息增益（取最大值）	取值多的属性增益偏大；树可能庞大但深度浅；对数运算多	二叉树及多叉树
2	C4.5	信息增益率（取最大值）	用增益率抑制取值多的属性；计算量仍大	二叉树及多叉树
3	CART	基尼系数（取最小值）	以基尼代替熵；最小化不纯度；每次选择最优属性及其一个取值进行划分	二叉树

概念

• 节点（Node）：树中的每个点，根节点是起点，内部节点是决策点，叶节点是结果。
• 分支（Branch）：节点之间的路径。
• 分裂（Split）：根据特征将数据集分成子集。
• 纯度（Purity）：子集中样本类别一致性，越高越相似。

过程

本质是贪心算法：在每个节点选当前最优特征（最大增益 / 最小基尼），继续向下递归，逐步接近最优。

信息增益（ID3）

$$ \text{Gain}(D,a)=\text{Ent}(D)-\sum_{v=1}^{V}\frac{|D_v|}{|D|}\text{Ent}(D_v) $$

• $a$：属性，假定有 $V$ 种取值，可将 $D$ 划分为 $V$ 个分支；$\mathrm{Gain}(D, a)$ 为划分得到的信息增益。
• $D_v$：属性 $a$ 的某个取值 $a_v$ 对应的分支集合。
• $\mathrm{Ent}(D)$：划分前的信息熵。
• $\sum_{v=1}^{V} \frac{|D_v|}{|D|} \mathrm{Ent}(D_v)$：划分后的条件熵。

信息增益率（C4.5）

信息增益对多取值属性偏好，增益率用于惩罚：

$$ \text{GainRatio}(D,a)=\frac{\text{Gain}(D,a)}{\text{IV}(a)} $$

其中

$$ \mathrm{IV}(a) = - \sum_{v=1}^{V} \frac{|D^v|}{|D|} \ln \frac{|D^v|}{|D|} $$

基尼指数（CART）

$$ \begin{aligned} \mathrm{Gini}(D) &= \sum_{k=1}^{|\mathcal{Y}|} \sum_{k' \neq k} p_k p_{k'} \ &= 1 - \sum_{k=1}^{|\mathcal{Y}|} p_k^2. \end{aligned} $$

数据越纯，$Gini$ 越小，只有一个类别时 $Gini=0$。

$$ \text{Gini\_{index}}(D, a)=\sum_{v=1}^V \frac{|{D^v}|}{|D|}\text{Gini}(D^v). $$

最优属性：$a_* = \underset{a \in A}{\arg\min} \, \mathrm{Gini\_index}(D, a)$。

伪代码

构建树(D):
    如果已纯净 → 停止
    如果无特征可分 → 停止
    否则：
        选最佳特征 a*
        按 a* 划分 D → {D1, D2, ...}
        对每个子集递归构建子树

剪枝

（记录待补充：预剪枝 / 后剪枝策略、验证集误差对比。）

---

机器学习：随机森林

CSDN参考资料

（待补充：Bagging 思路、特征采样、OOB 误差。）

XGBoost

（待补充：一阶/二阶泰勒展开、正则项、Shrinkage、列采样。）