生成模型

部分前置知识，参考 MCM-Week6

生成模型

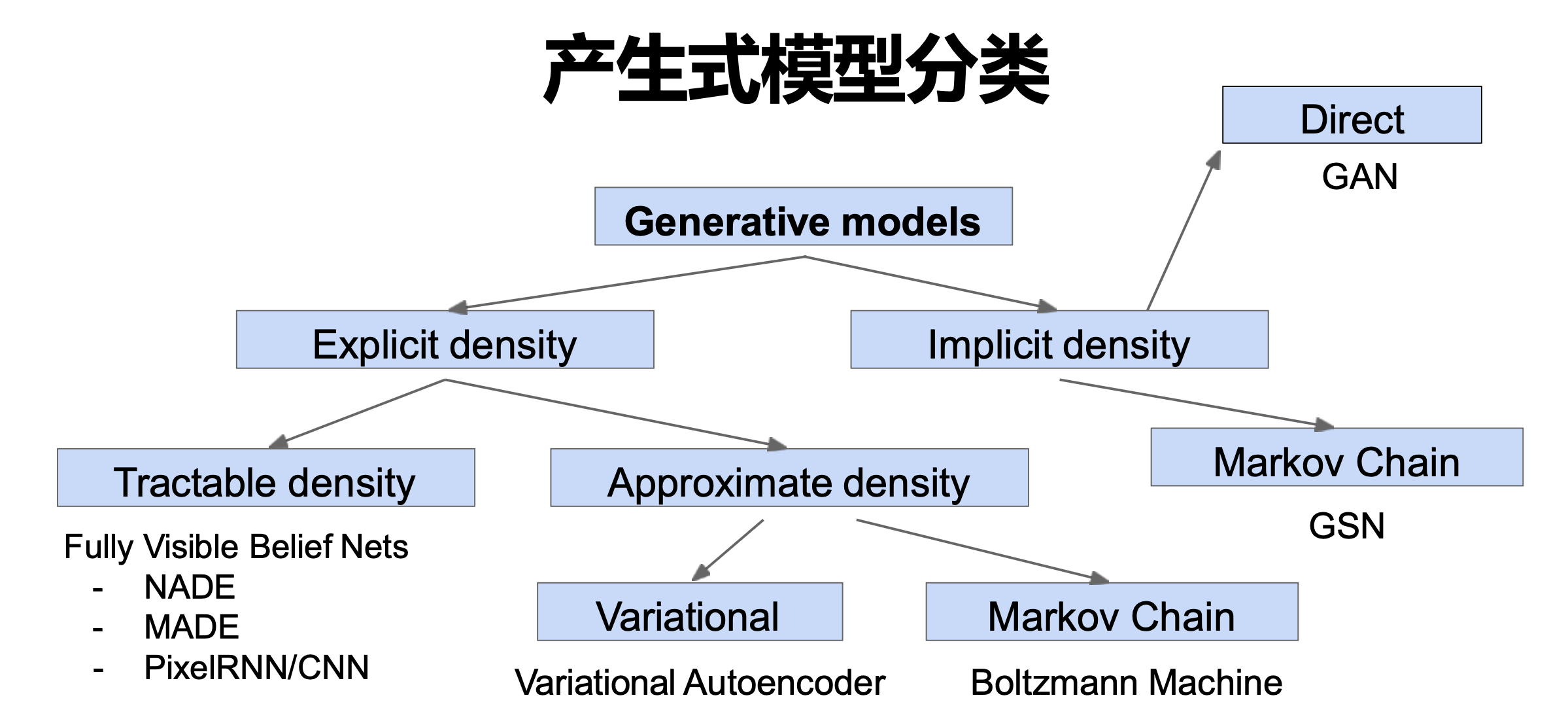
反向传播 Backpropagation

BP 网络的输入输出关系实质上是一种映射关系：一个 $n$ 输入 $m$ 输出的 BP 神经网络所完成的功能是从 $n$ 维欧氏空间向 $m$ 维欧氏空间中一有限域的连续映射，这一映射具有高度非线性。

简单非线性函数的多次复合，具有很强的函数复现能力。

设网络共有 $L$ 层（第 $L$ 层为输出层），输入为 $x$，标签为 $y$。

---

0. 记号约定

• 第 $l$ 层的参数：权重 $W^{(l)}$，偏置 $b^{(l)}$
• 第 $l$ 层的线性输出（未过激活）：$z^{(l)}$
• 第 $l$ 层的激活输出：$a^{(l)}$
• 激活函数：$\sigma(\cdot)$，导数：$\sigma'(\cdot)$
• 输入层输出定义为：$a^{(0)} = x$

---

1. 前向传播（Forward）

对 $l = 1,2,\dots,L$，逐层计算：

$$ z^{(l)} = W^{(l)} a^{(l-1)} + b^{(l)} $$

$$ a^{(l)} = \sigma\!\big(z^{(l)}\big) $$

最终网络输出为：

$$ \hat{y} = a^{(L)} $$

---

2. 损失函数（Loss）

若使用平方误差（教材常见）：

$$ L = \sum_i \big(\hat{y}_i - y_i\big)^2 $$

（也可写成向量形式：$L=\|\hat{y}-y\|_2^2$）

---

3. 反向传播（Backward）

引入误差信号（delta）：

$$ \delta^{(l)} \triangleq \frac{\partial L}{\partial z^{(l)}} $$

3.1 输出层误差

先算输出层对激活的导数，再乘激活函数导数（链式法则）：

$$ \delta^{(L)} = \frac{\partial L}{\partial a^{(L)}} \odot \sigma'\!\big(z^{(L)}\big) $$

对于平方误差 $L=\sum_i(\hat{y}_i-y_i)^2$，有：

$$ \frac{\partial L}{\partial a^{(L)}} = 2\big(a^{(L)} - y\big) $$

因此：

$$ \delta^{(L)} = 2\big(a^{(L)} - y\big)\odot \sigma'\!\big(z^{(L)}\big) $$

其中 $\odot$ 表示按元素相乘（Hadamard 乘积）。

3.2 隐藏层误差递推

对 $l = L-1, L-2, \dots, 1$：

$$ \delta^{(l)} = \big(W^{(l+1)}\big)^{\mathsf T}\delta^{(l+1)} \odot \sigma'\!\big(z^{(l)}\big) $$

---

4. 梯度计算（Gradients）

当 $\delta^{(l)}$ 已知时，第 $l$ 层的参数梯度为：

$$ \frac{\partial L}{\partial W^{(l)}} = \delta^{(l)} \big(a^{(l-1)}\big)^{\mathsf T} $$

$$ \frac{\partial L}{\partial b^{(l)}} = \delta^{(l)} $$

---

5. 参数更新（Update）

使用最基础的梯度下降（Gradient Descent），学习率为 $\eta$：

$$ W^{(l)} \leftarrow W^{(l)} - \eta \frac{\partial L}{\partial W^{(l)}} $$

$$ b^{(l)} \leftarrow b^{(l)} - \eta \frac{\partial L}{\partial b^{(l)}} $$

---

6. 训练停止条件（Stopping）

常见停止方式：

• 损失 $L$ 下降到足够小（达到阈值）
• 验证集指标不再提升（early stopping）
• 达到预设轮数（epochs）或迭代次数（iterations）

VAE Variational Auto-EnCoder

2013

参考资料：北京邮电大学 鲁鹏 生成模型

自编码器。做特征学习。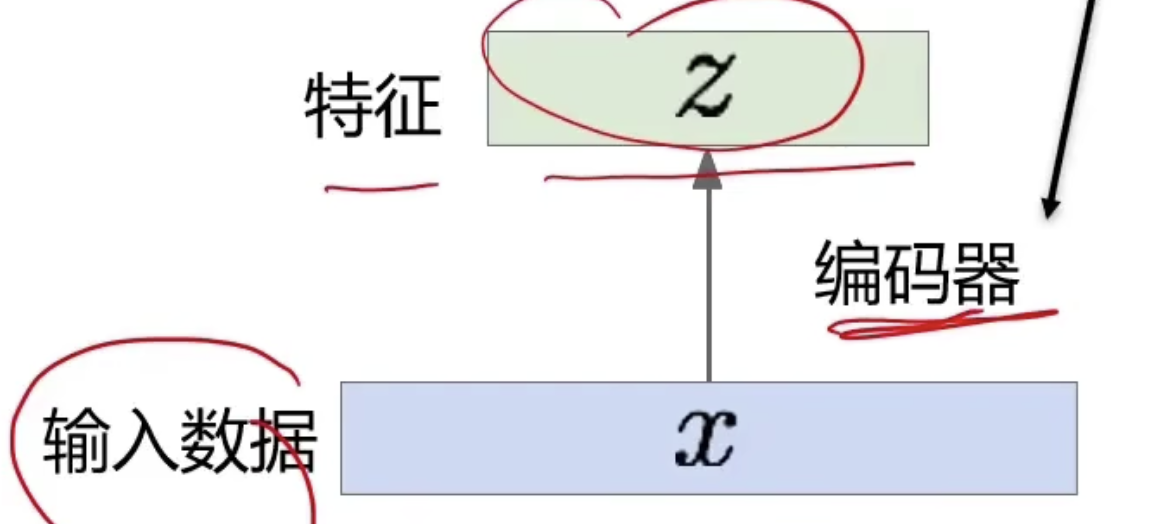 卷积神经网络，ReLU,CNN.

fully-connected。输入 $\to$ encoder $\to$ decoder 应该一样。

端到端训练，输入输出方差，loss 调整编码器、解码器。无监督。

VAE。

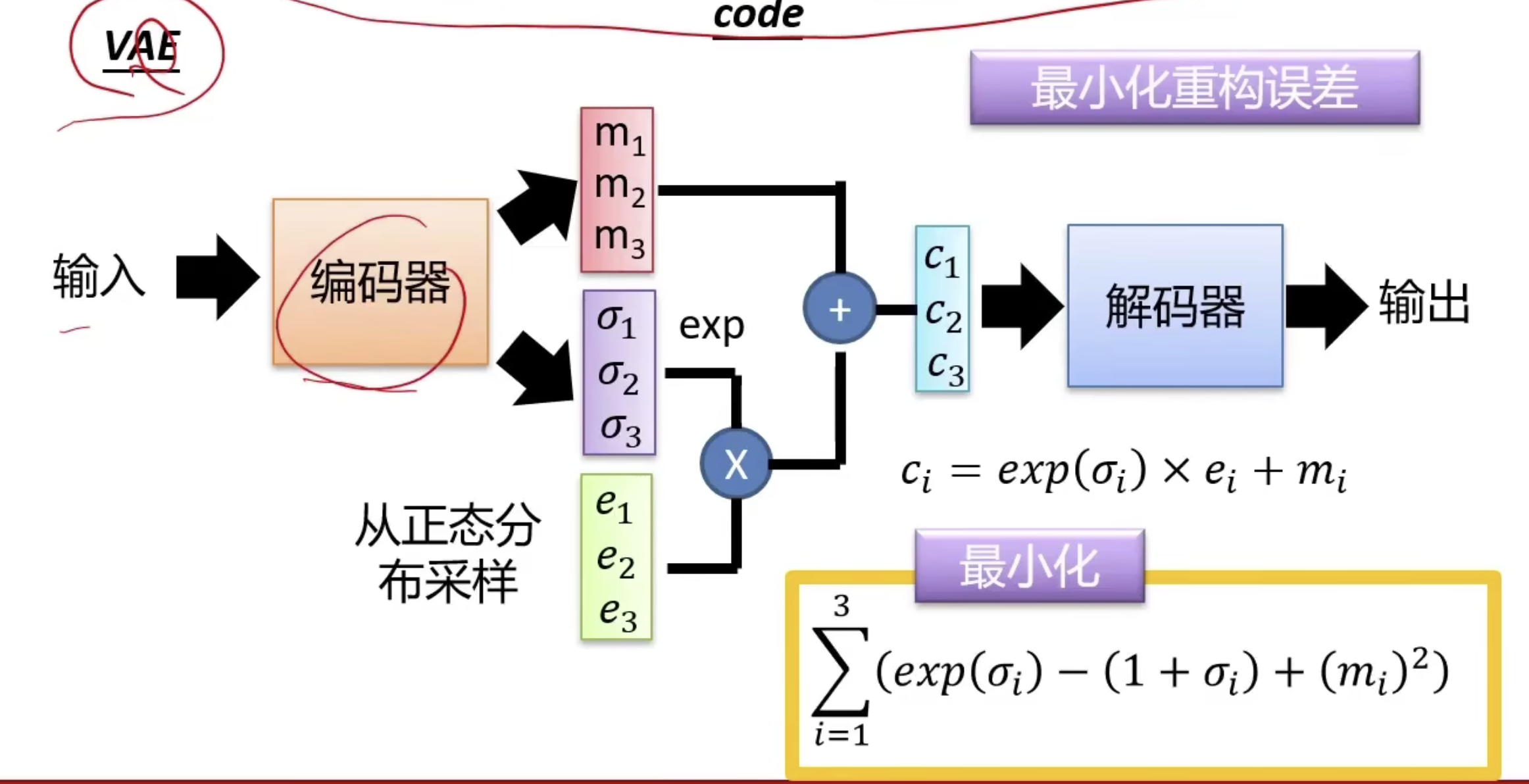
目标

$$\max_{\theta,\phi}\; \mathbb E_{q_\phi(z\mid x)}[\log p_\theta(x\mid z)]\;-\; \mathrm{KL}\big(q_\phi(z\mid x)\,\|\,p(z)\big)$$

$m$ - 原始编码 / $\sigma$ - 噪声 / $e$ - 以 $m$ 为中心的正态分布的随机采样

最终的数据 $c$ 是原始编码加上一个噪声。

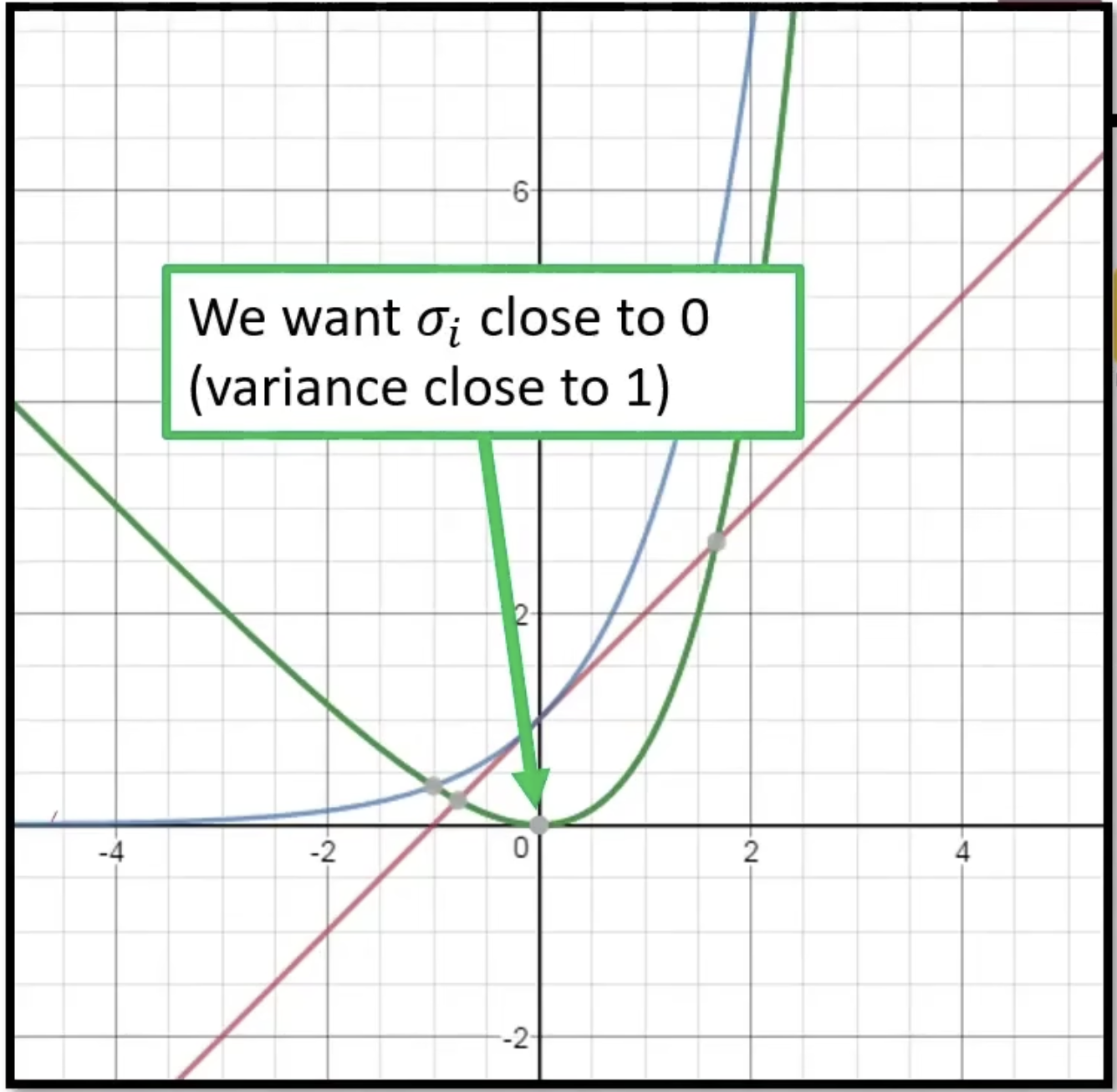
$\sigma$ 满足最小化公式 $KL$ 正则。按照图上来，$\sigma$ 应该是趋近于 1.

$$\sum_i\big(\exp(\sigma_i)-(1+\sigma_i)+m_i^2\big)$$

$(m_{i})^2$ L2 正则化，不让前面变量变得太大的惩罚。

推导。

高斯混合模型 - $P(x) = \sum_{m} P(m)P(x\mid m)$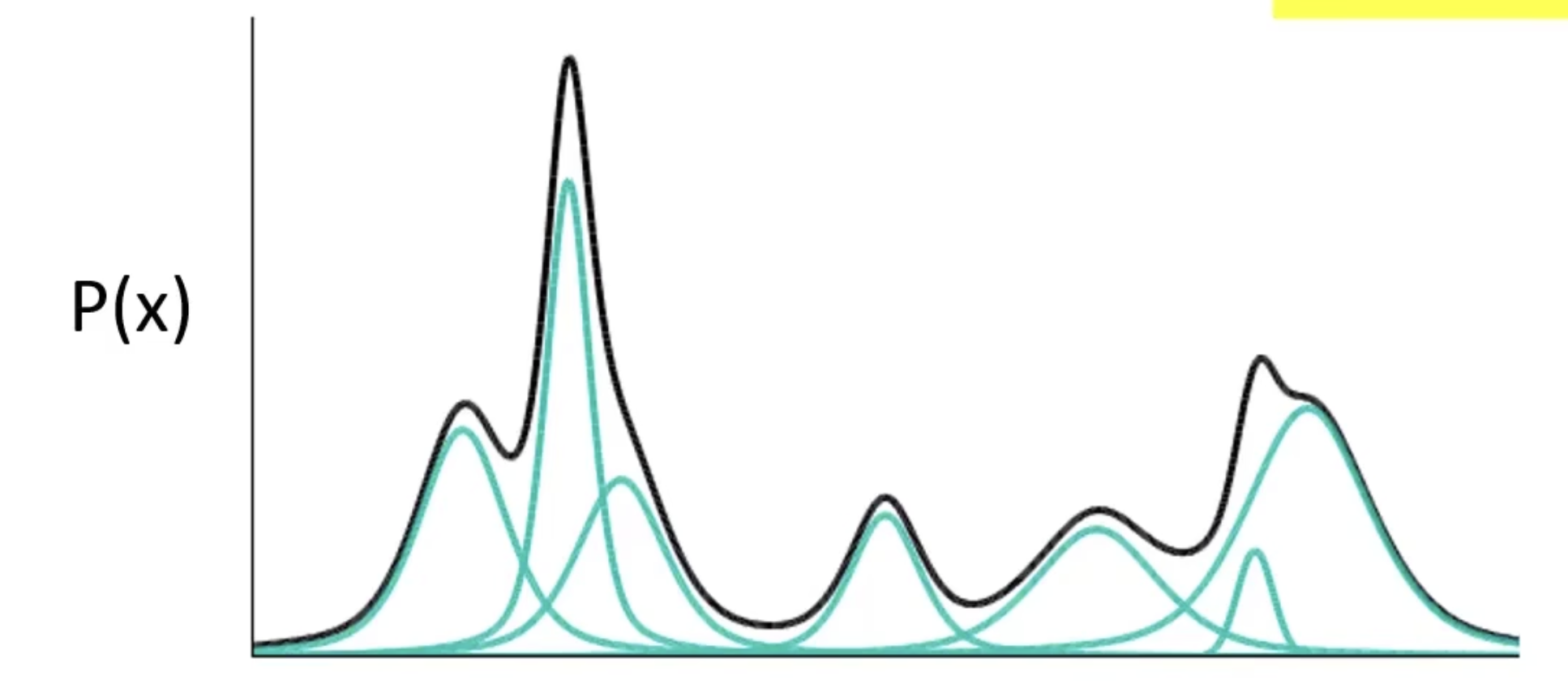

采样 $m \sim P(m)$ 多项式分布， $x\mid m \sim N(\mu^m,\Sigma^m)$

VAE，用无限高斯。用神经网络学习出无限个高斯组件。 $z \sim \mathcal N(0,I), \quad x\mid z \sim \mathcal N(\mu(z), \sigma(z))$

然后边缘分布变成积分： $p(x)=\int p(z)\,p(x\mid z)\,dz$

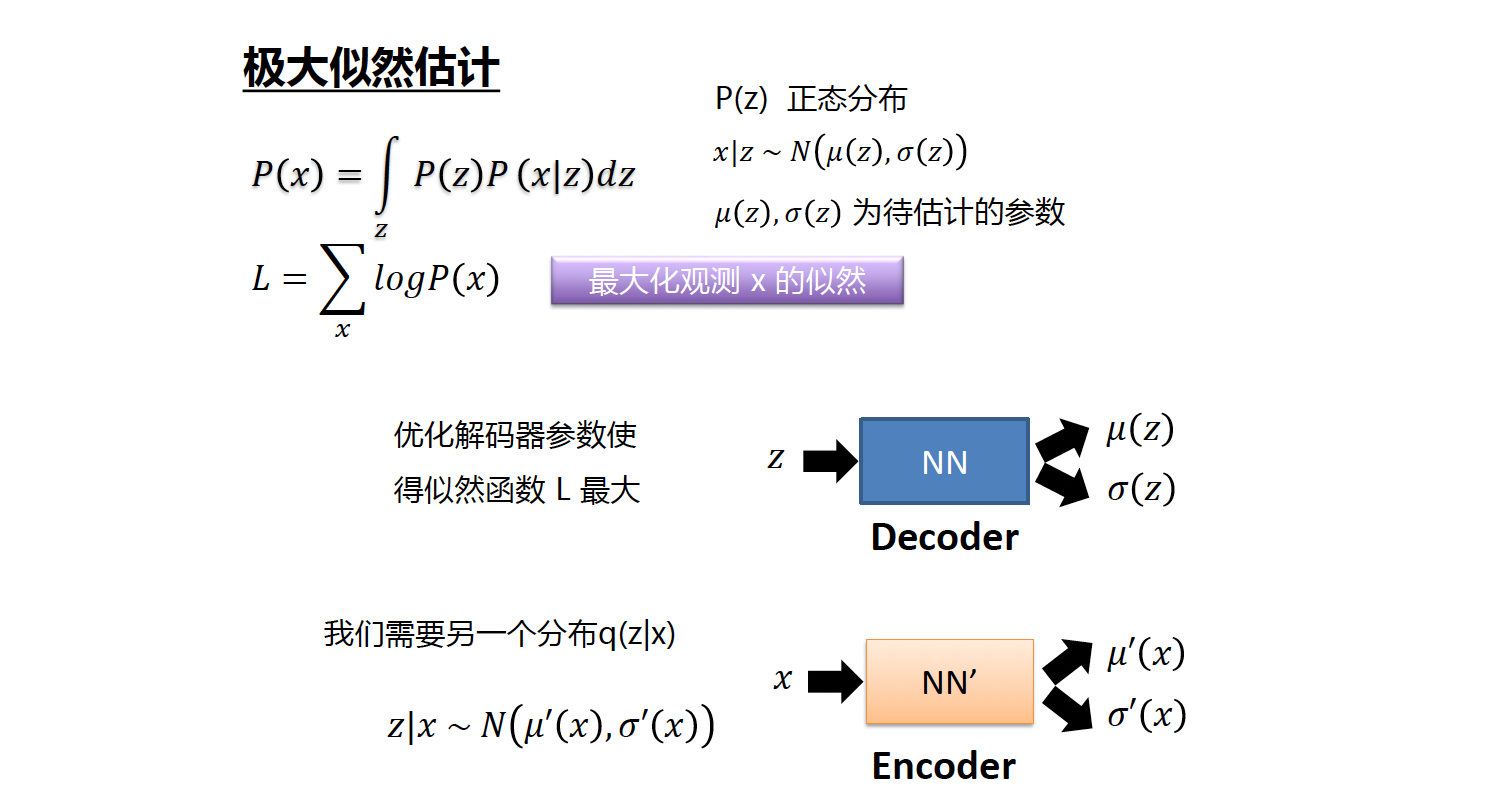
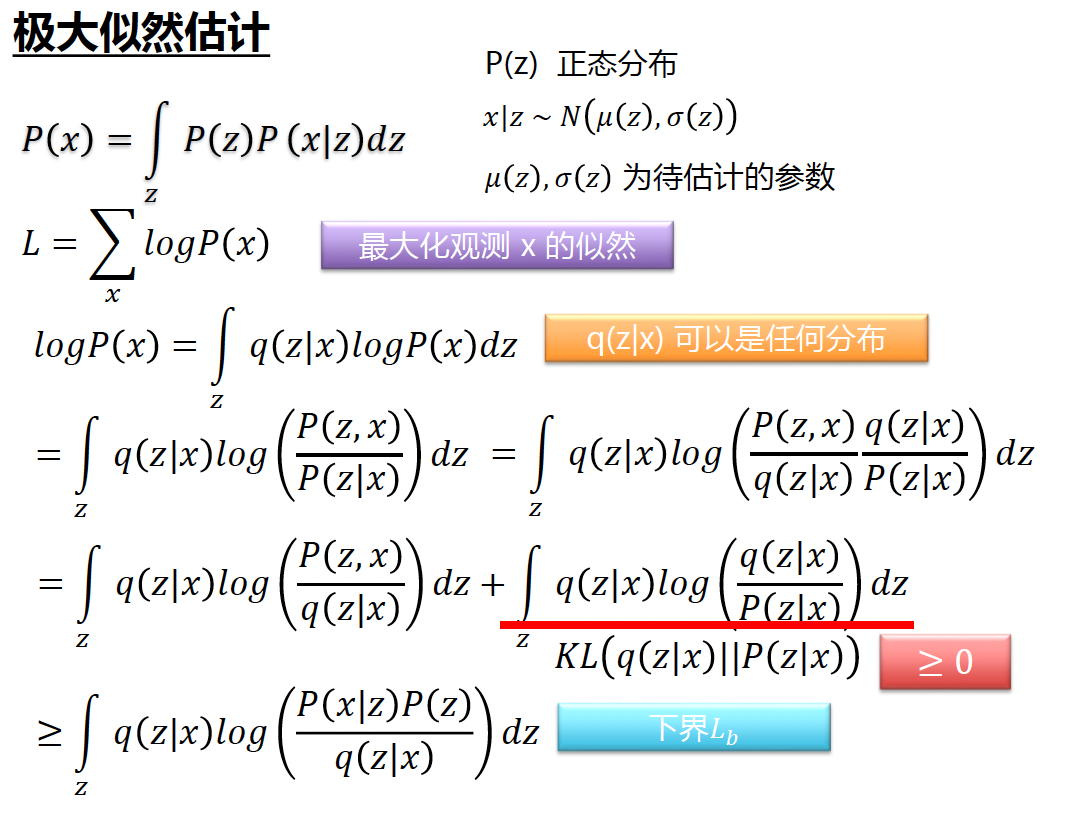
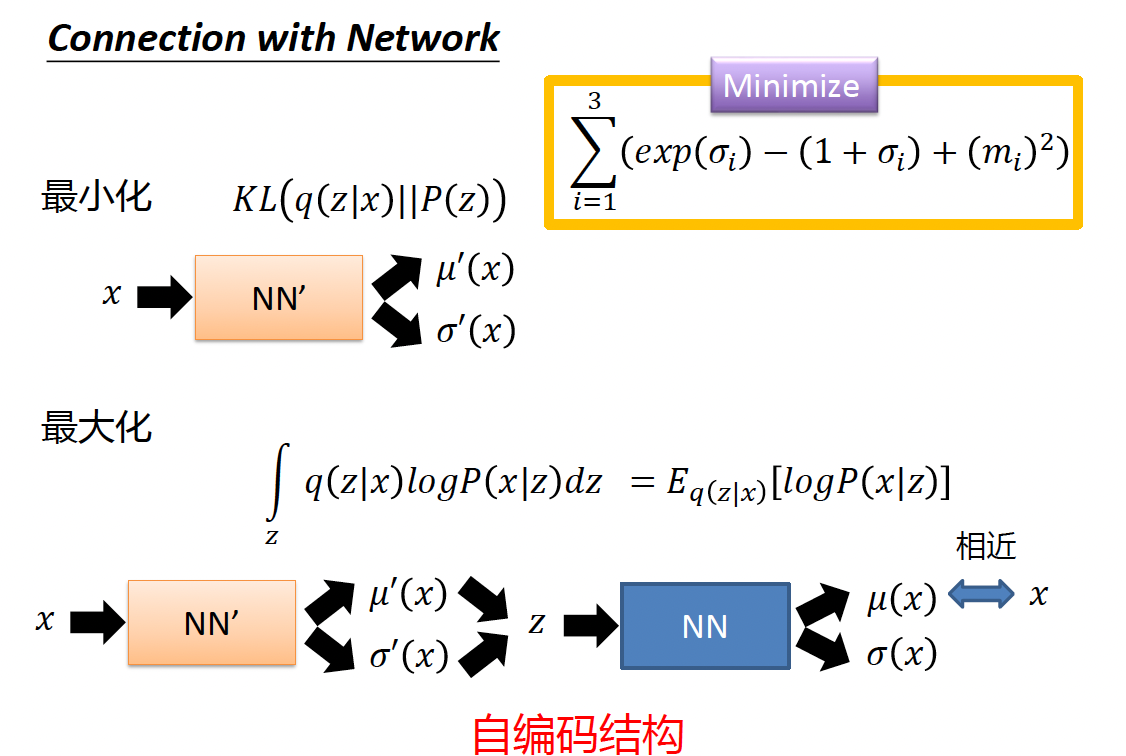
近似解

扩散模型

特殊的 VAE。

一个分布可以通过不断地添加噪声变成另一个分布。放到图像生成任务里，就是来自训练集的图像可以通过不断添加噪声变成符合标准正态分布的图像。从这个角度出发，我们可以对 VAE 做以下修改：1）不再训练一个可学习的编码器，而是把编码过程固定成不断添加噪声的过程；2）不再把图像压缩成更短的向量，而是自始至终都对一个等大的图像做操作。解码器依然是一个可学习的神经网络，它的目的也同样是实现编码的逆操作。不过，既然现在编码过程变成了加噪，那么解码器就应该负责去噪。而对于神经网络来说，去噪任务学习起来会更加有效。因此，扩散模型既不会涉及 GAN 中复杂的对抗训练，又比 VAE 更强大一点。

1）前向链（加噪）是固定的、已知的。 通常为高斯分布（正态分布）。

2）反向链（去噪/生成）是要学习的。（不准确？

QUOTE

生成扩散模型的大火，则是始于 2020 年所提出的 DDPM（Denoising Diffusion Probabilistic Model），虽然也用了”扩散模型”这个名字，但事实上除了采样过程的形式有一定的相似之外，DDPM 与传统基于朗之万方程采样的扩散模型可以说完全不一样，这完全是一个新的起点、新的篇章。【科学空间/9119】

Markov Chain：下一步只依赖上一步。 $p(x_t\mid x_{t-1},\dots,x_0)=p(x_t\mid x_{t-1}).$

DDPM Denoising Diffusion Probabilistic Model

2020.

我们的目标是学习如何从 $x_t$ 推导出 $p_{\theta}(x_{t-1}\mid x_{t})$ ，然后可以从这个分布中随机出一个 $x_{t-1} \,.$ （让每次输出的东西都是具有随机性的）（是扩散模型比 GAN 模型好的一个地方）

前向过程（加噪）

$$\mathbf{x}_t = \sqrt{\alpha_t} \mathbf{x}_{t-1} + \sqrt{\beta_t} \epsilon_t, \quad \epsilon_t \sim \mathcal{N}(0, \mathbf{I}\big)$$

$$q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) = \mathcal{N}\big(\sqrt{1 - \beta_t}\mathbf{x}_{t-1}, \beta_t \mathbf{I}\big)$$

$\mathcal N$ 高斯分布。

根据高斯分布的叠加性质，可以直接写出 $q(\mathbf{x}_t \mid \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t) \mathbf{I})$ 其中 $\bar{\alpha}_t=\prod_{i=1}^t \alpha_i$ .

后验分布推导

通过贝叶斯公式得到 $q(\mathbf{x}_{t-1} \mid \mathbf{x}_t) = \Large \frac{q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) q(\mathbf{x}_{t-1})}{q(\mathbf{x}_t)}$，其中，$q(\mathbf{x}_{t}\mid\mathbf{x}_{t-1})$ 是增噪过程，是显然的。

另外两项，添加一项 $x_0$，有 $q(\mathbf{x}_{t-1} \mid \mathbf{x}_0, \mathbf{x}_t) = \Large \frac{q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) q(\mathbf{x}_{t-1} \mid \mathbf{x}_0)}{q(\mathbf{x}_t \mid \mathbf{x}_0)} \,.$

带回去，

$$q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\mu}_t, \tilde{\beta}_t \mathbf{I})$$

后验均值 (Posterior Mean):

$$\tilde{\mu}_t = \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t} \mathbf{x}_0$$

后验方差 (Posterior Variance):

$$\tilde{\beta}_t = \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \beta_t$$

反向过程

目标函数：$\tilde{\mu}(\mathbf{x}_0, \mathbf{x}_t) = \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0 + \frac{\sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t \,.$

要有一个优化指标，跟 VAE，AE 没什么大的区别，$\|\mathbf{x}_{t-1} - \mu(\mathbf{x}_t)\|^2$，$\mathbf{x}_{t-1} \sim \mathcal{N}(\tilde{\mu}_t, \tilde{\beta}_t \mathbf{I})$ 。

重参数化：从预测 $\mathbf{x}_0$ 到预测噪声 $\epsilon$

由前向过程 $q(\mathbf{x}_t \mid \mathbf{x}_0)$ 可以写出：

$$\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\,\epsilon, \quad \epsilon \sim \mathcal{N}(0, \mathbf{I})$$

反过来，把 $\mathbf{x}_0$ 用 $\mathbf{x}_t$ 和 $\epsilon$ 表示：

$$\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}\big(\mathbf{x}_t - \sqrt{1-\bar{\alpha}_t}\,\epsilon\big)$$

代入后验均值 $\tilde{\mu}_t$ 的表达式，整理得：

$$\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}}\Big(\mathbf{x}_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\epsilon\Big)$$

所以问题转化了：不需要直接预测 $\mathbf{x}_0$ 或 $\tilde{\mu}_t$，只需要训练一个网络 $\epsilon_\theta(\mathbf{x}_t, t)$ 去预测加进去的那个噪声 $\epsilon$。预测出噪声之后，均值就能算出来：

$$\mu_\theta(\mathbf{x}_t, t) = \frac{1}{\sqrt{\alpha_t}}\Big(\mathbf{x}_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\epsilon_\theta(\mathbf{x}_t, t)\Big)$$

简化损失函数

完整的变分下界（ELBO）推导会得到一堆 KL 散度项，但 DDPM 的作者发现，把损失简化成下面这个形式效果最好：

$$L_{\text{simple}} = \mathbb{E}_{t, \mathbf{x}_0, \epsilon}\Big[\|\epsilon - \epsilon_\theta(\mathbf{x}_t, t)\|^2\Big]$$

就是让网络预测的噪声和真实加入的噪声之间的 MSE。$t$ 从 $\{1,2,\dots,T\}$ 中均匀采样。简单粗暴，但效果好。

训练算法

1. 从训练集采样 $\mathbf{x}_0 \sim q(\mathbf{x}_0)$
2. 均匀采样时间步 $t \sim \text{Uniform}(\{1,\dots,T\})$
3. 采样噪声 $\epsilon \sim \mathcal{N}(0, \mathbf{I})$
4. 用前向公式算出 $\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\,\epsilon$
5. 计算损失 $\|\epsilon - \epsilon_\theta(\mathbf{x}_t, t)\|^2$，梯度下降更新 $\theta$

不需要真的跑 $T$ 步加噪，一步就能从 $\mathbf{x}_0$ 跳到任意 $\mathbf{x}_t$（因为高斯的叠加性质）。

采样算法（生成过程）

从纯噪声开始，逐步去噪：

1. 采样 $\mathbf{x}_T \sim \mathcal{N}(0, \mathbf{I})$
2. 对 $t = T, T-1, \dots, 1$：
   • 如果 $t > 1$，采样 $\mathbf{z} \sim \mathcal{N}(0, \mathbf{I})$；否则 $\mathbf{z} = 0$
   • $\mathbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}}\Big(\mathbf{x}_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\epsilon_\theta(\mathbf{x}_t, t)\Big) + \sqrt{\tilde{\beta}_t}\,\mathbf{z}$
3. 输出 $\mathbf{x}_0$

最后一步（$t=1$）不加噪声，因为已经到终点了。每一步去噪都会加一点随机性（$\mathbf{z}$ 项），这就是扩散模型生成多样性的来源。

网络结构与超参数

DDPM 原文用的是 U-Net 作为噪声预测网络 $\epsilon_\theta$，时间步 $t$ 通过 sinusoidal position embedding 编码后注入网络。$T=1000$，$\beta$ 从 $\beta_1=10^{-4}$ 线性增长到 $\beta_T=0.02$。