
丙午马年,万事如意
2026 农历新年贺词,马年大吉,一马当先。

2026 农历新年贺词,马年大吉,一马当先。
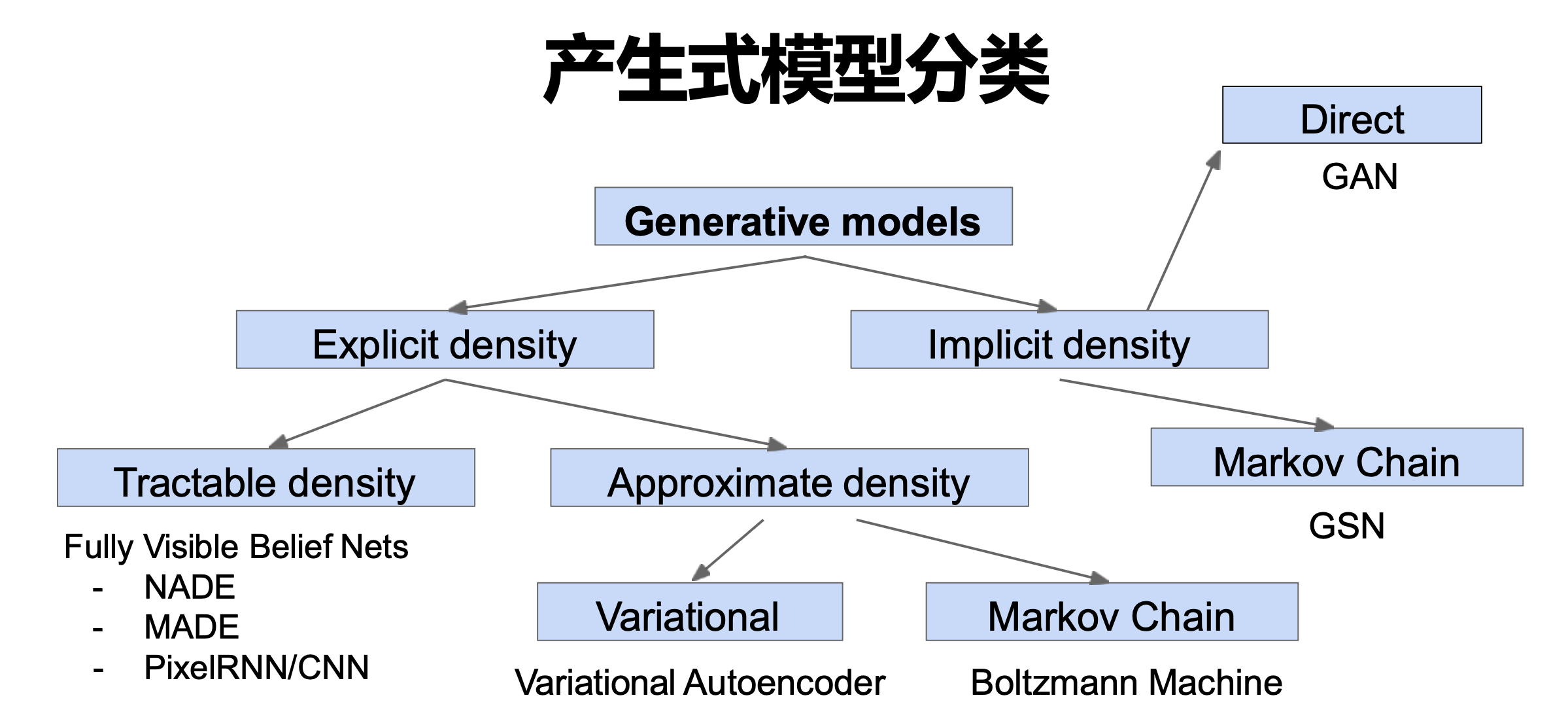
生成模型笔记:反向传播、VAE、扩散模型与 DDPM。

随笔,梳理一下最近一个月的见闻。

通过Tampermonkey脚本将浙江大学iZJU PeopleSoft系统的课表导出为ICS格式文件,并导入到各种日历应用的详细教程。

新年好,我干了些没啥用的事情,新年快乐🎆👍

这是高一寒假部分,因为快到三年了感觉再拖会忘记,所以赶紧写出来。
Obsidian Callout 标注类型、语法技巧与图片排版速查。

对比 NotebookLM 与 Nano Banana Pro 的图片能力:PPT 生成、修图(增删/光影)、平面设计,以及“推理模型→图片模型”的 prompt 工作流。

COMAP MCM 2025 C 周会笔记:特征工程、PCA、z-score,最主要的内容是学习了监督学习、决策树等机器学习模型。

MM-Review, a multimodal academic peer-review benchmark that stresses structured reasoning and robustness.