2023/12/16 晚 (OTC+8)22:35
T1 Constructive Problems
题意描述:
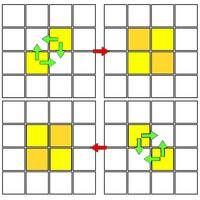
问如图方式填充一个 n\times m 的矩阵要预先填充多少个格子。
分析:
观察发现,每一列至少填充一个,才能构成条件,答案为 max(n,m)。
T2 Begginer’s Zelda
题意描述:
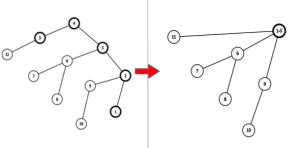
你可以把树的任意一条路径合并成一个点(如图),问多少次能将整棵树合并成一个点。
分析:
观察每次合并,最好的情况是包含两个叶子节点的合并。每次合并不会增加叶子节点,所以只要统计叶子节点总数。答案为 \lfloor (sum+1)/2\rfloor。
T3 Largest Subsequence
题意描述:
每次进行操作:找出字符串中字典序最大的子序列,并将其循环右移一位。问几次操作后序列为有序,或无法有序。
分析:
手模几次观察规律,如果可以使序列变为有序,所有的位移仅存在于最初始的最大字典序子序列上。
一个字符串中最大字典序的子序列一定是不递增的,所以倒着枚举出不递减子序列即可。根据这个性质,我们发现每次右移必须松弛一个字符,也就是初始子序列中最后一位,即最小一位,若不能松弛(也就是转过来之后发现前面一位比它大),当前新增的字符的大小一定会更大,也就构不成有序。
观察松弛操作,发现是reverse,那么将子序列翻转,判断是否有序,若有序,答案为\texttt{子序列长度}-\texttt{第一个字符的数量}。
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define maxd(x, y) ((x) > (y) ? (x) : (y))
#define mind(x, y) ((x) < (y) ? (x) : (y))
const double eps = 1e-8;
const double pi = acos(-1.0);
int T;
const int MAXN = 2e5 + 10;
char s[MAXN], t[MAXN];
int n;
inline void init(){for(int i = 0; i <= n; i++) {s[i] = t[i] = 0;}}
/*
czddeneeeemigec
znmigec
ccddezeeeenmige
ccddeeeeeeznmig
*/
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
// freopen("C.in", "r", stdin);
cin >> T;
while(T--) {
cin >> n;
init();
cin >> s;
vector<int> indx;
char tmp = s[0];
int tot = 0;
char mox = 'a';
for(int i = n - 1; i >= 0; i--) {
if(s[i] >= mox) {
mox = s[i];
t[tot++] = s[i];
indx.emplace_back(i);
}
}
tot--;
int sz = tot;
while(tot >= 1 and t[tot] == t[tot - 1]) tot--;
int flag = 1;
for(int i = 0; i < indx.size(); i++) {
s[indx[i]] = t[sz - i];
}
for(int i = 1; i < n; i++) {
if(s[i] < s[i - 1]) flag = 0;
}
if(flag == 1) cout << tot << endl;
else cout << -1 << endl;
}
return 0;
}
T4 Cyclic MEX
题意描述:
给定集合 \lbrace 0, 1, 2, \ldots , n-1\rbrace 的一种排列,求该排列循环右移任意次数后 \sum^{n}_{i=1}mex[a_1,a_2,\ldots,a_i] 的最大值。
分析:
观察发现几个性质:
- 所有序列的MEX是不递减的。
- 每次循环也就是弹出第一个数字 x ,MEX小于 x 的序列不变,大于 x 的序列变为 x。
- 每次弹出第一个数字减少第一位的MEX值,后加上 n。
由于不递减,每次减少的第一位值都很好维护,而 n 是最大的,直接添加在最后。很容易想到使用 deque 维护这个状态,分别记录MEX的数值和个数。而每个数字只会被弹出一次,所以删除和添加的次数是 \mathcal{O}(n) 的。
Code:
#include<bits/stdc++.h>
using namespace std;
#define int long long//不开 long long 见祖宗
const int N = 1e6 + 10;
int T, n, a[N];
signed main()
{
ios::sync_with_stdio(false);//关流同步,或者scanf
cin.tie(nullptr);
cout.tie(nullptr);
cin >> T;
while(T--){
deque<pair<int, int>> q;//结构体也行,全局记得清空
cin >> n;
vector<int> stat(n + 1);//注意初始化,以及空间,开大了会T
int pos = 0;
int cnt = 0, ans = 0;
for(int i = 1; i <= n; i++) {
cin >> a[i];
stat[a[i]] = 1;
while(stat[pos]) pos++;
q.push_back({pos, 1});
cnt += pos;
}
ans = cnt;
// cout << ans << endl;
for(int i = 1; i < n; i++) {
cnt -= q.front().first;
pair<int, int> now = {a[i], 0};
q.front().second--;
if(q.front().second == 0) {
q.pop_front();
}
while(!q.empty() && q.back().first > a[i]) {
cnt -= q.back().first * q.back().second;
now.second += q.back().second; q.pop_back();
}
q.push_back(now);
cnt += now.first * now.second;
q.push_back({n, 1});
cnt += n;
ans = max(ans, cnt);
}
cout << ans << endl;
}
return 0;
}
